Giải Bài Toán Tìm 2 Số Khi Biết Tổng Và Hiệu Chuẩn Xác Nhất

Chào bạn,

Có bao giờ bạn gặp phải tình huống cần Tìm 2 Số Khi Biết Tổng Và Hiệu của chúng chưa? Nghe qua có vẻ đơn giản, nhưng đây lại là một trong những dạng bài toán kinh điển, là nền tảng vững chắc cho rất nhiều kiến thức toán học phức tạp hơn sau này, thậm chí là cách tư duy giải quyết vấn đề trong cuộc sống và công việc. Dù bạn là học sinh đang làm quen với dạng bài này, phụ huynh muốn ôn tập cùng con, hay đơn giản là một người muốn “khơi lại” kiến thức cũ, bài viết này sẽ cùng bạn đi từ A đến Z, khám phá bí mật đằng sau bài toán thú vị này.

Chúng ta sẽ không chỉ học thuộc lòng công thức, mà còn đào sâu vào cách hiểu bản chất, tại sao công thức lại như vậy, và làm thế nào để áp dụng nó một cách linh hoạt nhất. Hãy cùng bắt đầu hành trình làm chủ bài toán tìm 2 số khi biết tổng và hiệu ngay bây giờ nhé!

Bài Toán Tìm 2 Số Khi Biết Tổng Và Hiệu Là Gì?

Nói một cách đơn giản nhất, bài toán tìm 2 số khi biết tổng và hiệu là dạng toán yêu cầu chúng ta xác định giá trị cụ thể của hai số chưa biết, dựa trên hai thông tin đã cho: tổng của hai số đó (khi cộng chúng lại) và hiệu của hai số đó (khi lấy số lớn trừ đi số bé).

Dạng toán này xuất hiện khá sớm trong chương trình giáo dục phổ thông, thường là ở cấp tiểu học. Nó giúp các em học sinh làm quen với việc biểu diễn các mối quan hệ giữa các đại lượng bằng toán học và phát triển khả năng suy luận logic. Mặc dù có vẻ cơ bản, nhưng việc nắm vững cách tìm 2 số khi biết tổng và hiệu là bước đệm quan trọng để tiếp cận các bài toán phức tạp hơn, bao gồm cả việc thiết lập và giải các hệ phương trình đơn giản sau này.

Bạn có thể hình dung bài toán này giống như một thử thách nho nhỏ. Bạn được cho biết tổng số kẹo của An và Bình là bao nhiêu, và An nhiều hơn Bình bao nhiêu viên. Nhiệm vụ của bạn là tìm xem mỗi bạn có chính xác bao nhiêu viên kẹo. Đó chính là bản chất của việc tìm 2 số khi biết tổng và hiệu đấy! Việc giải quyết những bài toán tưởng chừng đơn giản này ở cấp độ cơ bản giúp rèn luyện tư duy phân tích và tổng hợp dữ liệu, một kỹ năng cực kỳ cần thiết, tương tự như khi bạn cần phân tích các yếu tố ảnh hưởng đến [kim ngạch xuất khẩu là gì] của một mặt hàng vậy. Cả hai đều đòi hỏi khả năng xử lý các con số và mối quan hệ giữa chúng để đưa ra kết luận chính xác.

Công Thức Vàng Để Giải Bài Toán Tổng Hiệu

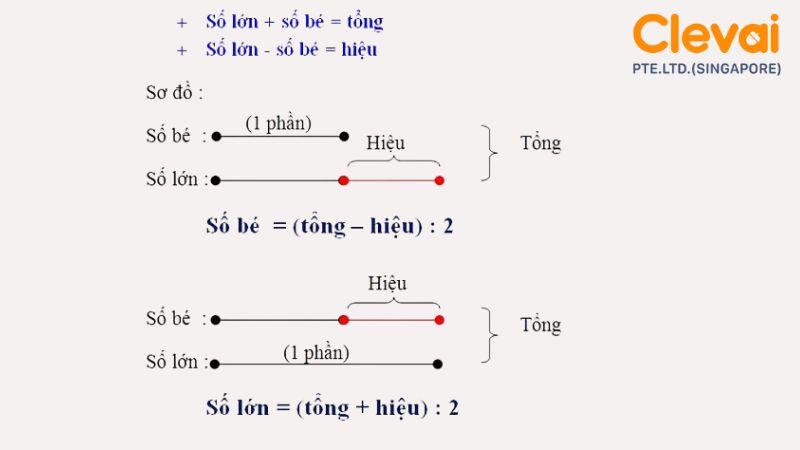
Để tìm 2 số khi biết tổng và hiệu, chúng ta có một cặp công thức cực kỳ quyền năng và dễ nhớ. Về cơ bản, cặp công thức này cho phép bạn tính ngay ra giá trị của từng số một cách trực tiếp.

Công thức đó là:

• Số lớn = (Tổng + Hiệu) : 2
• Số bé = (Tổng – Hiệu) : 2

Chỉ với hai công thức đơn giản này, mọi bài toán tìm 2 số khi biết tổng và hiệu đều có thể được giải quyết. Điều quan trọng là bạn cần xác định đúng đâu là tổng, đâu là hiệu và nhớ rằng hiệu luôn là kết quả của phép trừ số lớn cho số bé.

Để hiểu tại sao công thức này lại hoạt động, chúng ta có thể suy luận một chút. Giả sử số lớn là a và số bé là b.
Ta có:

1. a + b = Tổng (Theo định nghĩa tổng)
2. a - b = Hiệu (Theo định nghĩa hiệu, với a là số lớn)

Nếu ta cộng hai phương trình này lại với nhau:
(a + b) + (a - b) = Tổng + Hiệu
a + b + a - b = Tổng + Hiệu
2 * a = Tổng + Hiệu
a = (Tổng + Hiệu) : 2 (Đây chính là công thức tìm số lớn!)

Còn nếu ta lấy phương trình thứ nhất trừ đi phương trình thứ hai:
(a + b) - (a - b) = Tổng - Hiệu
a + b - a + b = Tổng - Hiệu
2 * b = Tổng - Hiệu
b = (Tổng - Hiệu) : 2 (Đây chính là công thức tìm số bé!)

Thật kỳ diệu phải không? Hai công thức này ra đời từ chính mối quan hệ cơ bản giữa tổng và hiệu của hai số. Việc hiểu được nguồn gốc này giúp bạn ghi nhớ công thức lâu hơn và tự tin hơn khi áp dụng.

{width=800 height=457}

Hướng Dẫn Chi Tiết Cách Tìm 2 Số Khi Biết Tổng Và Hiệu

Vậy, khi đối mặt với một bài toán cụ thể, chúng ta sẽ áp dụng công thức như thế nào? Quy trình giải bài toán tìm 2 số khi biết tổng và hiệu thường gồm các bước sau:

Các bước giải bài toán tìm hai số khi biết tổng và hiệu:

1. Đọc kỹ đề bài và xác định rõ Tổng và Hiệu: Đây là bước quan trọng nhất. Đề bài có thể cho trực tiếp tổng và hiệu, hoặc gián tiếp qua lời văn (ví dụ: “tổng hai số là…”, “số này hơn số kia…”, “hiệu của hai số là…”).
2. Áp dụng công thức tìm số lớn: Lấy Tổng cộng Hiệu, sau đó chia cho 2. Kết quả thu được chính là giá trị của số lớn.
3. Áp dụng công thức tìm số bé: Lấy Tổng trừ Hiệu, sau đó chia cho 2. Kết quả thu được chính là giá trị của số bé.
4. Kiểm tra lại kết quả: Đây là bước không thể thiếu để đảm bảo bạn đã giải đúng. Lấy hai số vừa tìm được cộng lại xem có bằng Tổng ban đầu không, và lấy số lớn trừ đi số bé xem có bằng Hiệu ban đầu không.

Ví dụ, đề bài cho: “Tổng hai số là 100, hiệu hai số là 20”.
Bước 1: Xác định Tổng = 100, Hiệu = 20.
Bước 2: Số lớn = (100 + 20) : 2 = 120 : 2 = 60.
Bước 3: Số bé = (100 – 20) : 2 = 80 : 2 = 40.
Bước 4: Kiểm tra: 60 + 40 = 100 (Đúng Tổng). 60 – 40 = 20 (Đúng Hiệu). Vậy kết quả 60 và 40 là chính xác.

Quy trình này rất mạch lạc và dễ theo dõi. Điều quan trọng là sự cẩn thận trong từng phép tính và không bỏ qua bước kiểm tra cuối cùng.

{width=800 height=450}

Ví Dụ Minh Họa Cụ Thể

Để làm quen hơn với cách áp dụng các công thức và quy trình, chúng ta hãy cùng xem xét một vài ví dụ minh họa từ đơn giản đến phức tạp hơn một chút. Việc thực hành qua các ví dụ là cách tốt nhất để nắm vững kỹ năng tìm 2 số khi biết tổng và hiệu.

Ví dụ 1: Bài toán cơ bản

Tổng của hai số là 150. Hiệu của hai số là 30. Tìm hai số đó.

• Xác định: Tổng = 150, Hiệu = 30.
• Số lớn = (150 + 30) : 2 = 180 : 2 = 90.
• Số bé = (150 – 30) : 2 = 120 : 2 = 60.
• Kiểm tra: 90 + 60 = 150; 90 – 60 = 30. (Kết quả đúng).
• Đáp số: Hai số cần tìm là 90 và 60.

Ví dụ 2: Bài toán với lời văn

Một thửa ruộng hình chữ nhật có chu vi là 240m. Chiều dài hơn chiều rộng 20m. Tính diện tích thửa ruộng đó.

Bài toán này yêu cầu tính diện tích, nhưng trước hết, chúng ta cần tìm chiều dài và chiều rộng của thửa ruộng. Đây chính là bài toán tìm 2 số khi biết tổng và hiệu ẩn dưới dạng lời văn.

• Xác định:
  • Chu vi hình chữ nhật = (Chiều dài + Chiều rộng) * 2.
  • Nửa chu vi = Chiều dài + Chiều rộng = 240m : 2 = 120m. Đây chính là Tổng của chiều dài và chiều rộng.
  • Chiều dài hơn chiều rộng 20m, tức là Hiệu của chiều dài và chiều rộng là 20m.
• Áp dụng công thức:
  • Chiều dài (số lớn) = (Nửa chu vi + Hiệu) : 2 = (120 + 20) : 2 = 140 : 2 = 70m.
  • Chiều rộng (số bé) = (Nửa chu vi – Hiệu) : 2 = (120 – 20) : 2 = 100 : 2 = 50m.
• Kiểm tra: Chiều dài + Chiều rộng = 70 + 50 = 120m (Đúng nửa chu vi). Chiều dài – Chiều rộng = 70 – 50 = 20m (Đúng hiệu).
• Tính diện tích: Diện tích = Chiều dài Chiều rộng = 70m 50m = 3500 mét vuông.
• Đáp số: Diện tích thửa ruộng là 3500 mét vuông.

Qua ví dụ này, bạn có thể thấy bài toán tìm 2 số khi biết tổng và hiệu có thể xuất hiện trong nhiều ngữ cảnh khác nhau. Điều quan trọng là khả năng “nhận diện” được dạng toán đó dựa trên các dữ kiện “tổng” và “hiệu” được cho, dù trực tiếp hay gián tiếp. Việc rèn luyện khả năng phân tích đề bài là chìa khóa để giải quyết thành công không chỉ bài toán này mà còn nhiều dạng toán khác. Kỹ năng phân tích này cũng là yếu tố cốt lõi khi làm việc tại một [công ty xuất nhập khẩu], nơi bạn phải xử lý rất nhiều thông tin khác nhau để đưa ra quyết định đúng đắn.

Ví dụ 3: Tổng và Hiệu là số thập phân

Tổng của hai số là 45.8. Hiệu của hai số là 12.2. Tìm hai số đó.

• Xác định: Tổng = 45.8, Hiệu = 12.2.
• Số lớn = (45.8 + 12.2) : 2 = 58 : 2 = 29.
• Số bé = (45.8 – 12.2) : 2 = 33.6 : 2 = 16.8.
• Kiểm tra: 29 + 16.8 = 45.8; 29 – 16.8 = 12.2. (Kết quả đúng).
• Đáp số: Hai số cần tìm là 29 và 16.8.

Ví dụ này chứng minh rằng công thức tìm 2 số khi biết tổng và hiệu vẫn hoàn toàn chính xác khi làm việc với các số không phải là số nguyên.

Ví dụ 4: Hiệu bằng 0

Tổng của hai số là 75. Hiệu của hai số là 0. Tìm hai số đó.

• Xác định: Tổng = 75, Hiệu = 0.
• Số lớn = (75 + 0) : 2 = 75 : 2 = 37.5.
• Số bé = (75 – 0) : 2 = 75 : 2 = 37.5.
• Kiểm tra: 37.5 + 37.5 = 75; 37.5 – 37.5 = 0. (Kết quả đúng).
• Đáp số: Hai số cần tìm là 37.5 và 37.5.

Trường hợp hiệu bằng 0 xảy ra khi hai số đó bằng nhau. Công thức của chúng ta vẫn cho ra kết quả đúng trong trường hợp đặc biệt này.

Qua các ví dụ trên, hy vọng bạn đã cảm thấy tự tin hơn khi áp dụng công thức tìm 2 số khi biết tổng và hiệu. Hãy luyện tập thật nhiều với các bài toán khác nhau để thành thạo nhé!

Tại Sao Bài Toán Tổng Hiệu Lại Quan Trọng?

Bạn có thể tự hỏi, tại sao một bài toán tưởng chừng chỉ dành cho học sinh tiểu học như việc tìm 2 số khi biết tổng và hiệu lại được nhắc đến nhiều như vậy và thậm chí còn được coi là nền tảng quan trọng?

Câu trả lời nằm ở giá trị tư duy mà nó mang lại. Bài toán này không chỉ đơn thuần là áp dụng công thức. Nó dạy cho chúng ta cách:

1. Phân tích dữ kiện: Từ một bài toán lời văn, chúng ta phải biết cách “bóc tách” thông tin để xác định đâu là Tổng, đâu là Hiệu. Kỹ năng này rất cần thiết trong việc giải quyết mọi vấn đề, từ học tập đến công việc.
2. Biểu diễn mối quan hệ: Hiểu được rằng Tổng = Số lớn + Số bé, và Hiệu = Số lớn – Số bé. Đây là bước đầu tiên làm quen với việc mô hình hóa các vấn đề bằng toán học.
3. Sử dụng công cụ (công thức): Áp dụng công thức một cách chính xác để tìm ra ẩn số.
4. Kiểm tra và xác nhận: Bước kiểm tra giúp củng cố kết quả và rèn luyện tính cẩn thận.

Thầy Nguyễn Văn A – Giáo viên Toán Tiểu học với hơn 20 năm kinh nghiệm chia sẻ: “Bài toán tìm 2 số khi biết tổng và hiệu là viên gạch đầu tiên trong việc xây dựng tư duy đại số cho học sinh. Nó giúp các con hình dung ra mối quan hệ giữa các số thông qua phép cộng và trừ, tạo tiền đề vững chắc để tiếp cận các bài toán về hệ phương trình sau này. Việc nắm vững công thức và hiểu được bản chất của bài toán này là cực kỳ quan trọng.”

Thực tế, ý tưởng đằng sau việc tìm 2 số khi biết tổng và hiệu – tức là sử dụng hai phương trình độc lập (một liên quan đến tổng, một liên quan đến hiệu hay sự khác biệt) để tìm ra hai ẩn số – là nguyên tắc cơ bản của việc giải hệ phương trình bậc nhất hai ẩn. Dù ở cấp tiểu học chúng ta chưa gọi tên, nhưng đây chính là bước chân đầu tiên vào thế giới đại số.

Ngay cả trong các lĩnh vực đòi hỏi tính toán phức tạp, như phân tích dữ liệu hay quản lý tài chính, nguyên tắc cơ bản của việc cân bằng và giải quyết các mối quan hệ giữa các biến số vẫn dựa trên những nền tảng toán học cơ bản nhất, bao gồm cả khả năng làm việc với tổng và hiệu.

{width=800 height=600}

Những Lỗi Thường Gặp Khi Giải Bài Toán Tìm 2 Số Khi Biết Tổng Và Hiệu

Mặc dù công thức tìm 2 số khi biết tổng và hiệu khá đơn giản, nhưng trong quá trình giải bài tập, học sinh (và cả người lớn!) vẫn có thể mắc phải một số sai lầm phổ biến. Nhận biết được những lỗi này sẽ giúp chúng ta cẩn thận hơn và tránh được chúng.

Dưới đây là một số lỗi thường gặp:

• Nhầm lẫn giữa Tổng và Hiệu: Đây là lỗi cơ bản nhất. Đôi khi, đề bài cho hai số, và người giải nhầm lẫn giữa số lớn và số bé để tính hiệu, hoặc đơn giản là đọc sai đề bài.
• Áp dụng sai công thức: Nhầm lẫn giữa công thức tìm số lớn và số bé, hoặc quên chia cho 2 sau khi cộng hoặc trừ. Ví dụ, tính (Tổng + Hiệu) mà quên chia 2 để ra số lớn.
• Tính toán sai: Dù công thức đúng, nhưng thực hiện các phép cộng, trừ, chia bị sai. Lỗi này thường xảy ra khi làm việc với số lớn, số thập phân, hoặc khi vội vàng.
• Quên bước kiểm tra: Không kiểm tra lại kết quả cuối cùng bằng cách lấy hai số vừa tìm được cộng và trừ lại để so sánh với Tổng và Hiệu ban đầu. Bước này cực kỳ quan trọng để phát hiện sớm các sai lầm.
• Xác định sai Tổng hoặc Hiệu trong bài toán lời văn: Như ví dụ về thửa ruộng hình chữ nhật ở trên, “Tổng” được cho dưới dạng “nửa chu vi”, chứ không phải chu vi. Nếu không đọc kỹ và phân tích đề bài cẩn thận, rất dễ xác định sai Tổng hoặc Hiệu.

Để tránh những lỗi này, hãy luôn đọc đề bài thật kỹ, gạch chân các dữ kiện quan trọng (Tổng là bao nhiêu, Hiệu là bao nhiêu), viết rõ công thức trước khi áp dụng, thực hiện phép tính cẩn thận và luôn dành thời gian kiểm tra lại kết quả. Giống như việc kiểm tra lại các con số trong một bản khai báo, sự cẩn thận và tỉ mỉ là chìa khóa để có được kết quả chính xác.

Hiểu rõ công thức tính tần số trong vật lý cần sự chính xác từng bước, tương tự như việc áp dụng công thức tổng hiệu trong toán học. Mọi sai sót nhỏ trong quá trình tính toán đều có thể dẫn đến kết quả cuối cùng không chính xác.

Áp Dụng Bài Toán Tổng Hiệu Trong Đời Sống

Có thể bạn nghĩ, bài toán tìm 2 số khi biết tổng và hiệu chỉ nằm trong sách giáo khoa? Thực ra, nguyên tắc tư duy này có thể được áp dụng một cách ẩn dụ trong nhiều tình huống thực tế, ngay cả khi chúng ta không dùng công thức một cách trực diện.

Hãy thử nghĩ xem:

• Chia sẻ đồ vật: Bạn và em trai có tổng cộng 20 món đồ chơi. Bạn có nhiều hơn em trai 4 món. Hỏi mỗi người có bao nhiêu món? (Tổng = 20, Hiệu = 4).
• Ước tính thời gian: Tổng thời gian bạn dành cho việc học và chơi trong một ngày là 8 tiếng. Thời gian học nhiều hơn thời gian chơi 2 tiếng. Hỏi bạn học bao lâu và chơi bao lâu? (Tổng = 8 tiếng, Hiệu = 2 tiếng).
• Phân bổ nguồn lực: Hai dự án A và B được phân bổ tổng cộng 100 triệu đồng ngân sách. Dự án A nhận được nhiều hơn dự án B 10 triệu đồng. Hỏi ngân sách cho mỗi dự án là bao nhiêu? (Tổng = 100 triệu, Hiệu = 10 triệu).

Trong các ví dụ này, chúng ta đang sử dụng tư duy tìm 2 số khi biết tổng và hiệu để phân chia một tổng thể thành hai phần dựa trên sự chênh lệch giữa chúng. Dù có thể không cần viết công thức ra giấy, bộ não của chúng ta vẫn đang thực hiện các bước suy luận tương tự.

Ngay cả trong lĩnh vực xuất nhập khẩu, dù các phép tính có thể phức tạp hơn rất nhiều, nguyên tắc cơ bản của việc xử lý các đại lượng có mối quan hệ tổng và hiệu vẫn hiện hữu. Ví dụ, khi bạn cần xác định thành phần của một lô hàng dựa trên tổng trọng lượng và sự chênh lệch trọng lượng giữa hai loại hàng, bạn đang vô hình trung áp dụng tư duy giải bài toán tổng hiệu. Hiểu rõ [khối lượng tịnh là gì] và cách nó liên quan đến các loại khối lượng khác là một ví dụ về việc phân tích các đại lượng và mối quan hệ của chúng trong thực tế ngành XNK.

Lịch Sử Đơn Giản Của Bài Toán Tổng Hiệu

Khái niệm về tổng và hiệu của các con số đã tồn tại từ rất lâu đời, cùng với sự phát triển của toán học sơ cấp. Ngay từ khi con người bắt đầu biết đếm và thực hiện các phép tính cơ bản, nhu cầu phân chia hoặc so sánh các số lượng đã xuất hiện.

Các nền văn minh cổ đại như Ai Cập, Babylon đã có những hiểu biết sâu sắc về số học và đại số sơ khai, dù cách họ trình bày bài toán có thể khác với chúng ta ngày nay. Bài toán tìm 2 số khi biết tổng và hiệu về bản chất là một dạng đơn giản của bài toán giải hệ phương trình tuyến tính, một lĩnh vực đã được nghiên cứu và phát triển qua hàng nghìn năm bởi các nhà toán học từ khắp nơi trên thế giới.

Trong lịch sử toán học phương Đông, đặc biệt là ở Trung Quốc và Ấn Độ, các bài toán về tổng và hiệu cũng xuất hiện trong các văn bản cổ. Chúng thường được trình bày dưới dạng các bài toán thực tế liên quan đến phân chia tài sản, đo đạc đất đai, hoặc trao đổi hàng hóa. Cách giải ban đầu có thể dựa trên phương pháp “giả thiết tạm” hoặc biểu diễn bằng hình học, trước khi được hệ thống hóa thành các công thức đại số như chúng ta biết ngày nay.

Sự xuất hiện của bài toán tìm 2 số khi biết tổng và hiệu trong chương trình giáo dục hiện đại phản ánh tầm quan trọng của nó như một bước chuyển từ tư duy số học đơn thuần sang tư duy đại số trừu tượng hơn. Nó giúp học sinh làm quen với việc sử dụng ký hiệu (ví dụ: a, b) để biểu diễn các số chưa biết và thiết lập mối quan hệ giữa chúng.

Cô Lê Thị B – Chuyên viên Phân tích Dữ liệu tại một công ty công nghệ chia sẻ: “Nghe có vẻ lạ, nhưng ngay cả khi xử lý các tập dữ liệu lớn hay xây dựng các mô hình phức tạp, nền tảng tư duy từ những bài toán cơ bản như tìm tổng hiệu vẫn hữu ích. Nó rèn luyện khả năng nhìn nhận vấn đề dưới dạng các biến số và mối quan hệ giữa chúng. Một nhân viên xuất nhập khẩu giỏi cũng cần khả năng phân tích và giải quyết vấn đề dựa trên các dữ kiện cho sẵn, giống như cách chúng ta giải bài toán này vậy.”

Các Biến Thể Và Nâng Cao Của Bài Toán Tổng Hiệu

Bài toán tìm 2 số khi biết tổng và hiệu là dạng cơ bản nhất. Từ nền tảng này, toán học phát triển lên các dạng bài phức tạp hơn, nhưng vẫn dựa trên cùng một nguyên tắc tư duy về mối quan hệ giữa các số.

Một số biến thể và dạng nâng cao phổ biến bao gồm:

• Bài toán Tổng – Tỉ: Biết tổng của hai số và tỉ số giữa chúng (ví dụ: số này gấp mấy lần số kia, hoặc số này bằng bao nhiêu phần của số kia).
• Bài toán Hiệu – Tỉ: Biết hiệu của hai số và tỉ số giữa chúng.
• Bài toán Tổng – Hiệu – Tỉ (với ba số trở lên): Biết tổng, hiệu, và tỉ số giữa các cặp số trong một nhóm ba số trở lên.

Cách giải các bài toán này thường phức tạp hơn, có thể liên quan đến việc vẽ sơ đồ đoạn thẳng để biểu diễn mối quan hệ giữa các số, hoặc sử dụng phương trình đại số. Tuy nhiên, điểm chung là chúng đều yêu cầu khả năng phân tích dữ kiện, xác định mối quan hệ giữa các số (tổng, hiệu, tỉ lệ), và áp dụng các phương pháp phù hợp để tìm ra các số chưa biết.

Ví dụ, trong bài toán Tổng – Tỉ, nếu biết Tổng là S và số lớn gấp k lần số bé (số lớn / số bé = k), ta có hệ:
Số lớn + Số bé = S
Số lớn = k * Số bé

Thay phương trình thứ hai vào phương trình thứ nhất:
(k Số bé) + Số bé = S
(k + 1) Số bé = S
Số bé = S / (k + 1)
Từ đó tìm ra Số lớn = k * Số bé.

Bạn thấy đó, ngay cả khi không phải là bài toán tổng hiệu trực tiếp, việc hiểu cách biến đổi và kết hợp các phương trình vẫn dựa trên tư duy giải quyết vấn đề từ những nền tảng cơ bản nhất. Nắm vững cách tìm 2 số khi biết tổng và hiệu chính là bước đệm vững chắc để bạn chinh phục các dạng toán nâng cao hơn này.

Lời Khuyên Từ “Người Đi Trước” Khi Học Bài Toán Này

Nếu bạn đang học hoặc hướng dẫn ai đó học bài toán tìm 2 số khi biết tổng và hiệu, đây là vài lời khuyên nho nhỏ có thể giúp ích:

1. Hiểu bản chất, đừng học vẹt: Cố gắng hiểu tại sao công thức lại như vậy, thay vì chỉ học thuộc lòng. Việc chứng minh lại công thức một vài lần sẽ giúp bạn ghi nhớ lâu hơn và linh hoạt hơn khi áp dụng.
2. Vẽ sơ đồ: Đặc biệt với các bài toán lời văn, việc vẽ sơ đồ đoạn thẳng biểu diễn Tổng và Hiệu (hoặc số lớn, số bé) có thể giúp bạn hình dung rõ hơn mối quan hệ giữa các đại lượng và tránh nhầm lẫn.
3. Luyện tập đa dạng: Đừng chỉ làm đi làm lại một dạng bài. Tìm các bài toán có số liệu khác nhau (số nguyên, số thập phân), các dạng lời văn khác nhau để rèn luyện khả năng phân tích đề bài.
4. Đừng sợ sai: Sai là chuyện bình thường khi học. Điều quan trọng là sau khi sai, bạn tìm hiểu nguyên nhân vì sao sai và sửa lại cho đúng.
5. Luôn kiểm tra lại: Tạo thói quen kiểm tra lại kết quả sau mỗi bài toán. Chỉ mất vài giây nhưng giúp bạn chắc chắn rằng mình đã làm đúng.

Việc học toán cũng giống như xây một ngôi nhà, cần có nền móng vững chắc. Bài toán tìm 2 số khi biết tổng và hiệu chính là một trong những viên gạch nền móng quan trọng đó. Hãy kiên nhẫn, luyện tập chăm chỉ, và bạn sẽ thấy nó không hề khó chút nào!

Tổng Kết Lại Cách Tìm 2 Số Khi Biết Tổng Và Hiệu

Vậy là chúng ta đã cùng nhau khám phá khá kỹ về bài toán tìm 2 số khi biết tổng và hiệu. Hy vọng rằng, sau bài viết này, bạn đã nắm vững công thức, hiểu rõ cách áp dụng, và nhận ra tầm quan trọng của nó trong việc xây dựng tư duy toán học.

Nhắc lại một lần nữa, công thức cốt lõi để tìm 2 số khi biết tổng và hiệu là:

• Số lớn = (Tổng + Hiệu) : 2
• Số bé = (Tổng – Hiệu) : 2

Các bước thực hiện bao gồm: Xác định Tổng và Hiệu, áp dụng công thức tính số lớn, áp dụng công thức tính số bé, và kiểm tra lại kết quả.

Dù bạn gặp bài toán này ở trường, trong sách vở, hay trong một tình huống thực tế cần phân chia, hãy nhớ rằng đây là một dạng bài cơ bản nhưng cực kỳ hữu ích. Việc nắm vững cách tìm 2 số khi biết tổng và hiệu không chỉ giúp bạn giải quyết các bài toán cụ thể mà còn rèn luyện khả năng phân tích, suy luận và giải quyết vấn đề, những kỹ năng cần thiết cho mọi lĩnh vực trong cuộc sống.

Hãy bắt tay vào thực hành ngay hôm nay để củng cố kiến thức này nhé!