Công Thức Tính Hình Tròn: Khám Phá Từ A-Z Công Việc Hàng Ngày

Xin chào mừng bạn đến với Tài Liệu XNK! Hôm nay, chúng ta sẽ cùng nhau “lặn sâu” vào một chủ đề tưởng chừng quen thuộc nhưng lại vô cùng quan trọng trong cuộc sống và công việc: Công Thức Tính Hình Tròn. Chắc hẳn, ngay từ những năm ngồi trên ghế nhà trường, chúng ta đã được làm quen với những ký hiệu như π (pi), r, d, S, P… Nhưng bạn có bao giờ tự hỏi, tại sao những công thức này lại xuất hiện, chúng có ý nghĩa gì sâu xa hơn là chỉ để giải bài tập trong sách giáo khoa, và làm thế nào để áp dụng chúng một cách hiệu quả nhất trong đời sống hay thậm chí là trong những lĩnh vực chuyên môn như xuất nhập khẩu hay kỹ thuật?

Trong bài viết này, chúng ta sẽ không chỉ nhắc lại những kiến thức cơ bản về công thức tính hình tròn mà còn cùng nhau khám phá nguồn gốc, ý nghĩa, và vô vàn ứng dụng thực tế của chúng, từ việc đơn giản như tính diện tích chiếc bánh pizza cho đến những bài toán phức tạp trong xây dựng, kỹ thuật hay thậm chí là thiết kế. Hãy cùng bắt đầu hành trình giải mã “vũ trụ hình tròn” này nhé!

Giới thiệu về Hình Tròn và các Công Thức Tính Hình Tròn Cơ Bản

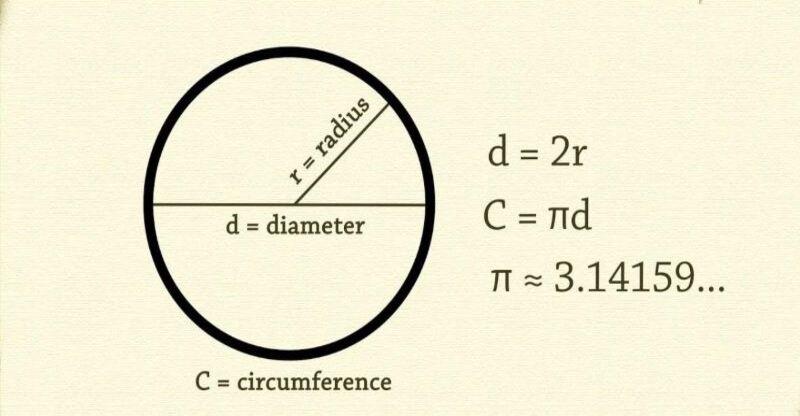
Trước khi đi sâu vào các phép tính, chúng ta cần hiểu rõ hình tròn là gì và những thành phần cấu tạo nên nó. Một cách đơn giản nhất, hình tròn là tập hợp tất cả các điểm cách đều một điểm cố định (gọi là tâm) một khoảng không đổi. Khoảng cách không đổi này chính là bán kính của hình tròn, thường được ký hiệu là r hoặc R.

Đường kính của hình tròn, ký hiệu là d hoặc D, là đoạn thẳng đi qua tâm và nối hai điểm bất kỳ trên đường tròn. Dễ thấy, đường kính luôn gấp đôi bán kính, tức là d = 2r.

Hai đại lượng quan trọng nhất mà chúng ta thường cần tính toán khi làm việc với hình tròn là Chu vi và Diện tích.

Chu vi (ký hiệu C hoặc P) là độ dài “đường viền” xung quanh hình tròn. Tưởng tượng bạn đi bộ dọc theo mép của một hồ nước hình tròn, tổng quãng đường bạn đi chính là chu vi của hồ nước đó.

Diện tích (ký hiệu S hoặc A) là toàn bộ “không gian” mà hình tròn chiếm chỗ trên một mặt phẳng. Nếu hồ nước đó có đáy hình tròn, diện tích đáy chính là diện tích hình tròn.

Và để tính toán hai đại lượng này, chúng ta cần một hằng số toán học đặc biệt: số Pi (π). Pi là một con số vô tỷ (không thể biểu diễn dưới dạng phân số đơn giản) và là một trong những hằng số quan trọng nhất trong toán học. Giá trị xấp xỉ thường dùng của Pi là 3.14 hoặc 22/7, nhưng trong tính toán khoa học, người ta dùng giá trị chính xác hơn (ví dụ: 3.14159…). Pi có một mối liên hệ kỳ diệu với hình tròn: tỷ lệ giữa chu vi của bất kỳ hình tròn nào với đường kính của nó luôn bằng Pi. Tức là, C / d = π, suy ra C = πd. Vì d = 2r, nên chúng ta có công thức tính chu vi hình tròn theo bán kính: C = 2πr.

Đối với diện tích, công thức tính được phát hiện sau chu vi khá lâu và cũng dựa trên hằng số Pi. Công thức tính diện tích hình tròn là S = πr² (hoặc A = πR²). Đây là những công thức cơ bản nhất về công thức tính hình tròn mà chúng ta cần ghi nhớ.

{width=800 height=533}

Trước khi đi sâu vào chi tiết từng công thức và ứng dụng của chúng, có lẽ bạn cũng sẽ thấy thú vị khi tìm hiểu về những khái niệm tính toán khác, chẳng hạn như cách cân bằng các yếu tố trong một hệ thống phức tạp, tương tự như cách người ta áp dụng công thức tính cán cân xuất nhập khẩu để đánh giá tình hình thương mại của một quốc gia. Mặc dù khác lĩnh vực, nhưng nguyên lý sử dụng công thức để hiểu và phân tích một đối tượng là hoàn toàn tương đồng.

Tại sao cần nắm vững các Công Thức Tính Hình Tròn?

Bạn có nghĩ rằng công thức tính hình tròn chỉ dành cho học sinh hay các nhà toán học? Hoàn toàn không! Nắm vững những công thức này mang lại vô vàn lợi ích thiết thực trong cuộc sống và công việc.

Thứ nhất, nó giúp chúng ta giải quyết các bài toán thực tế. Bạn muốn biết cần bao nhiêu mét rào để quây quanh một khu vườn hình tròn? Bạn cần tính diện tích mặt bàn tròn để mua khăn trải bàn phù hợp? Bạn muốn biết chiếc bánh xe của bạn đi được bao xa sau mỗi vòng quay? Tất cả đều cần đến công thức tính hình tròn.

Thứ hai, nó là nền tảng cho nhiều lĩnh vực khoa học và kỹ thuật. Từ thiết kế các bộ phận máy móc có dạng tròn (bánh răng, vòng bi, ống dẫn) đến tính toán diện tích bề mặt hoặc thể tích của các vật thể hình trụ, hình nón, hình cầu (đều có liên quan mật thiết đến hình tròn), kiến thức về công thức tính hình tròn là không thể thiếu. Các kiến trúc sư sử dụng nó để thiết kế các công trình có yếu tố cong, các kỹ sư sử dụng nó để tính toán sức bền vật liệu, các nhà vật lý sử dụng nó để mô tả chuyển động tròn hay sóng.

Thứ ba, nó rèn luyện khả năng tư duy logic và giải quyết vấn đề. Việc hiểu và áp dụng công thức đòi hỏi bạn phải phân tích bài toán, xác định thông tin đã biết (bán kính hay đường kính?), lựa chọn công thức phù hợp và thực hiện các bước tính toán chính xác. Đây là kỹ năng quan trọng không chỉ trong toán học mà còn trong mọi khía cạnh của cuộc sống.

Cuối cùng, đôi khi, việc hiểu rõ công thức tính hình tròn còn giúp bạn tránh được những sai lầm ngớ ngẩn trong cuộc sống thường ngày. Ví dụ, bạn mua một chiếc quạt trần có đường kính cánh quạt là 1.2m, bạn cần biết nó sẽ làm mát được một khu vực có diện tích khoảng bao nhiêu để đặt đúng vị trí trong phòng. Công thức diện tích hình tròn sẽ giúp bạn trả lời câu hỏi này.

Nói tóm lại, công thức tính hình tròn không chỉ là những công thức khô khan trong sách vở mà là chìa khóa để mở cánh cửa hiểu biết và giải quyết nhiều vấn đề trong thế giới xung quanh chúng ta.

{width=800 height=533}

Đi sâu vào từng Công Thức Tính Hình Tròn: Chu Vi

Công Thức Tính Chu Vi Hình Tròn Là Gì?

Công thức tính chu vi hình tròn biểu thị độ dài đường biên của hình tròn. Nó cho biết quãng đường bạn sẽ đi nếu di chuyển một vòng quanh mép của hình tròn đó.

Công thức tính chu vi hình tròn có hai dạng cơ bản, dựa trên bán kính hoặc đường kính.

Công thức theo bán kính r là: C = 2πr

Công thức theo đường kính d là: C = πd

Như đã giải thích ở trên, vì đường kính d luôn gấp đôi bán kính r (d = 2r), nên hai công thức này thực chất là một. Công thức C = πd trực tiếp thể hiện định nghĩa của số Pi (π) là tỷ lệ giữa chu vi và đường kính của bất kỳ hình tròn nào.

Tại Sao Công Thức Chu Vi Lại Là C = 2πr hay C = πd?

Lịch sử tìm ra công thức chu vi hình tròn đã có từ rất lâu đời, gắn liền với quá trình con người khám phá ra số Pi. Các nền văn minh cổ đại như Ai Cập, Babylon, Hy Lạp đều nhận thấy rằng tỷ lệ giữa chu vi và đường kính của hình tròn là một hằng số, mặc dù giá trị Pi mà họ sử dụng không chính xác bằng ngày nay.

Nhà toán học Hy Lạp cổ đại Archimedes là một trong những người đầu tiên đưa ra phương pháp tính toán giá trị của Pi một cách có hệ thống bằng cách sử dụng các đa giác nội tiếp và ngoại tiếp đường tròn. Ông đã chứng minh rằng tỷ lệ chu vi trên đường kính nằm giữa 3 + 10/71 và 3 + 1/7 (tức là giữa 3.1408 và 3.1428).

Công thức C = πd (hoặc C = 2πr) là kết quả trực tiếp từ định nghĩa của Pi. Nếu Pi được định nghĩa là tỷ lệ C/d, thì nhân d lên hai vế ta được C = πd. Đơn giản vậy thôi!

Ứng Dụng Thực Tế Của Công Thức Chu Vi

Công thức tính chu vi hình tròn có rất nhiều ứng dụng trong cuộc sống hàng ngày và các ngành nghề khác nhau:

• Xây dựng và Kiến trúc: Tính độ dài các thanh uốn cong theo hình tròn (lan can cầu thang, khung cửa sổ tròn), tính chu vi móng cọc hình tròn, tính độ dài đường viền trang trí hình tròn.
• Cơ khí và Chế tạo: Tính chiều dài dây đai cần dùng cho các puly hình tròn, tính chu vi bánh răng để thiết kế hệ thống truyền động, tính chu vi ống dẫn để xác định lượng vật liệu bọc ngoài.
• Giao thông vận tải: Tính quãng đường xe đi được dựa trên chu vi bánh xe và số vòng quay. Nếu bánh xe có bán kính r, sau mỗi vòng quay nó đi được một quãng đường đúng bằng chu vi của nó (2πr).
• Nông nghiệp và Làm vườn: Tính lượng vật liệu cần thiết để làm hàng rào quanh khu đất hình tròn, tính chu vi miệng giếng tròn để làm thành.
• May mặc và Thủ công: Tính độ dài viền ren cần cho cổ áo tròn, tính chu vi vành nón, tính chiều dài dây trang trí cho vật dụng hình tròn.
• Thể thao: Tính chiều dài đường chạy trong sân vận động (thường có các khúc cua hình bán nguyệt), tính chu vi của các loại bóng (bóng rổ, bóng đá).

Ví dụ: Một chiếc bánh xe đạp có đường kính 66 cm. Để biết sau 100 vòng quay, bánh xe đi được bao nhiêu mét, ta cần tính chu vi của nó.
Chu vi C = πd = 3.14 66 cm = 207.24 cm.
Sau 100 vòng quay, quãng đường đi được là 100 207.24 cm = 20724 cm = 207.24 mét.

Việc tính toán này cần sự chính xác, giống như khi bạn cần tính tỉ lệ dân thành thị để phân tích cơ cấu dân số vậy, sai số nhỏ trong phép tính có thể dẫn đến kết quả cuối cùng khác biệt đáng kể.

{width=800 height=416}

Công Thức Tính Hình Tròn Quan Trọng Khác: Diện Tích

Công Thức Tính Diện Tích Hình Tròn Là Gì?

Công thức tính diện tích hình tròn cho biết toàn bộ không gian mà hình tròn chiếm giữ trên một mặt phẳng. Nó đo lường “độ lớn” của bề mặt bên trong đường biên hình tròn.

Công thức tính diện tích hình tròn chỉ có một dạng cơ bản theo bán kính r:

S = πr² (hoặc A = πR²)

Trong đó:

• S (hoặc A) là diện tích hình tròn.
• π (pi) là hằng số Pi (xấp xỉ 3.14 hoặc 22/7).
• r (hoặc R) là bán kính hình tròn.
• r² có nghĩa là r nhân r (bán kính bình phương).

Nếu bạn chỉ biết đường kính d, bạn có thể tính bán kính bằng cách chia đường kính cho 2 (r = d/2), sau đó áp dụng công thức S = π(d/2)² = π(d²/4). Dạng này ít phổ biến hơn nhưng cũng đúng.

Làm Thế Nào Để Hiểu Công Thức Diện Tích S = πr²?

Công thức diện tích hình tròn không hiển nhiên như công thức chu vi. Có nhiều cách để “chứng minh” hoặc trực quan hóa công thức này:

Một cách phổ biến là chia hình tròn thành nhiều hình quạt nhỏ bằng nhau, sau đó “xếp” chúng lại thành một hình gần giống hình bình hành hoặc hình chữ nhật. Khi số lượng hình quạt càng lớn, hình xếp được càng giống hình chữ nhật.

{width=800 height=504}

• “Chiều dài” của hình chữ nhật này sẽ là tổng độ dài của các cung tròn nhỏ, khi xếp lại gần bằng một nửa chu vi của hình tròn ban đầu, tức là (1/2) * 2πr = πr.
• “Chiều rộng” của hình chữ nhật này chính là chiều dài của bán kính hình quạt, tức là r.

Diện tích của hình chữ nhật được tính bằng chiều dài nhân chiều rộng. Do đó, diện tích hình tròn xấp xỉ bằng (πr) * r = πr². Khi số lượng hình quạt tiến tới vô cùng, hình xếp được chính xác là hình chữ nhật, và diện tích của nó chính là diện tích hình tròn.

Cách giải thích này giúp chúng ta dễ hình dung tại sao lại có π và r² trong công thức diện tích công thức tính hình tròn.

Ứng Dụng Thực Tế Của Công Thức Diện Tích

Công thức tính diện tích hình tròn cũng có vô vàn ứng dụng:

• Xây dựng: Tính diện tích bề mặt các cột trụ tròn, tính diện tích sàn nhà hình tròn, tính diện tích cần lát gạch cho khu vực hình tròn.
• Nông nghiệp: Tính diện tích mặt ao tròn để ước tính lượng cá nuôi, tính diện tích khu vực tưới nước của vòi phun xoay tròn.
• Thiết kế và Trang trí: Tính diện tích bề mặt cần sơn cho vật thể hình tròn, tính diện tích thảm tròn, tính diện tích bề mặt gương tròn.
• Ẩm thực: Tính diện tích chiếc bánh pizza để so sánh kích thước (một chiếc bánh đường kính 30cm có diện tích gấp bao nhiêu lần chiếc bánh đường kính 20cm?).
• Khoa học: Tính diện tích tiết diện ngang của ống dẫn để tính lưu lượng dòng chảy, tính diện tích bề mặt của tế bào hình cầu (liên quan đến diện tích hình tròn lớn nhất).
• Quy hoạch: Tính toán diện tích vùng ảnh hưởng của một trạm phát sóng hình tròn, tính toán mật độ dân số trong một khu vực có ranh giới hình tròn giả định.

Ví dụ: Bạn có một chiếc bàn tròn có đường kính 1.2 mét. Bạn muốn mua một tấm kính tròn để đặt lên mặt bàn. Cần tính diện tích mặt bàn để biết kích thước tấm kính.
Đường kính d = 1.2m, suy ra bán kính r = d/2 = 1.2m / 2 = 0.6m.
Diện tích S = πr² = 3.14 (0.6m)² = 3.14 0.36 m² = 1.1304 m².
Vậy bạn cần mua tấm kính có diện tích khoảng 1.13 m².

Việc tính toán này cần sự chính xác, giống như khi bạn cần tính toán các con số phức tạp trong công thức tính cán cân xuất nhập khẩu để đưa ra nhận định về nền kinh tế.

{width=800 height=499}

Làm thế nào để áp dụng Công Thức Tính Hình Tròn trong thực tế?

Áp dụng công thức tính hình tròn trong thực tế không khó, nhưng đòi hỏi sự cẩn thận và chú ý đến các bước sau:

1. Xác định rõ bạn cần tính gì: Bạn cần tính chu vi (độ dài đường viền) hay diện tích (bề mặt bên trong)?
2. Xác định thông tin đã biết: Bạn đã biết bán kính (r) hay đường kính (d)? Hoặc có thể bạn biết chu vi hay diện tích và cần tính ngược lại bán kính/đường kính?
3. Chọn công thức phù hợp:
   • Nếu cần tính chu vi và biết bán kính r: C = 2πr
   • Nếu cần tính chu vi và biết đường kính d: C = πd
   • Nếu cần tính diện tích và biết bán kính r: S = πr²
   • Nếu cần tính diện tích và biết đường kính d: S = π(d/2)² = πd²/4
   • Nếu biết chu vi C, muốn tính bán kính r: r = C / (2π)
   • Nếu biết chu vi C, muốn tính đường kính d: d = C / π
   • Nếu biết diện tích S, muốn tính bán kính r: r = √(S / π)
   • Nếu biết diện tích S, muốn tính đường kính d: d = 2 * √(S / π)
4. Kiểm tra đơn vị đo: Đảm bảo tất cả các đại lượng (bán kính, đường kính) đều cùng một đơn vị đo (ví dụ: cùng là centimet, cùng là mét). Diện tích sẽ có đơn vị là bình phương của đơn vị độ dài (cm², m², km²…), còn chu vi sẽ có đơn vị giống đơn vị độ dài (cm, m, km…). Đừng nhầm lẫn giữa cm và cm²!
5. Sử dụng giá trị Pi phù hợp: Đối với các bài toán phổ thông hoặc ước lượng nhanh, bạn có thể dùng π ≈ 3.14 hoặc 22/7. Đối với các tính toán cần độ chính xác cao (ví dụ: trong kỹ thuật, khoa học), hãy sử dụng giá trị Pi từ máy tính bỏ túi hoặc phần mềm chuyên dụng.
6. Thực hiện phép tính: Thay các giá trị đã biết vào công thức và tính toán. Sử dụng máy tính để có kết quả chính xác, đặc biệt với số Pi.
7. Kiểm tra kết quả: Kết quả có hợp lý không? Ví dụ, nếu bạn tính diện tích một chiếc nhẫn đeo tay và ra kết quả vài mét vuông thì rõ ràng là sai rồi!

Ví dụ thực hành từng bước:

• Bài toán 1: Một chiếc hồ cá cảnh hình tròn có bán kính 40 cm. Cần bao nhiêu mét dây đèn LED để viền quanh miệng hồ?

  1. Cần tính: Chu vi (độ dài đường viền).
  2. Đã biết: Bán kính r = 40 cm.
  3. Công thức phù hợp: C = 2πr.
  4. Đơn vị: cm. Kết quả chu vi sẽ là cm, cần đổi sang mét ở cuối.
  5. Tính toán: C = 2 3.14 40 cm = 251.2 cm.
  6. Đổi đơn vị: 251.2 cm = 2.512 mét.
  7. Kiểm tra: Chu vi xấp xỉ 2.5 mét có vẻ hợp lý cho một hồ cá cảnh.
  • Đáp số: Cần khoảng 2.512 mét dây đèn LED.

• Bài toán 2: Một sân chơi trẻ em hình tròn có đường kính 10 mét. Cần bao nhiêu mét vuông thảm cao su để phủ kín sân chơi?

  1. Cần tính: Diện tích (bề mặt bên trong).
  2. Đã biết: Đường kính d = 10 mét.
  3. Công thức phù hợp: S = π(d/2)² hoặc S = πr². Cần tính bán kính r = d/2 = 10m / 2 = 5m.
  4. Đơn vị: mét. Kết quả diện tích sẽ là mét vuông (m²).
  5. Tính toán: S = 3.14 (5m)² = 3.14 25 m² = 78.5 m².
  6. Kiểm tra: Diện tích 78.5 m² có vẻ hợp lý cho sân chơi đường kính 10m.
  • Đáp số: Cần khoảng 78.5 mét vuông thảm cao su.

Việc thực hành các ví dụ này giúp bạn làm quen với việc áp dụng công thức tính hình tròn một cách tự tin và chính xác hơn. Giống như việc luyện tập cách viết email tiếng anh vậy, càng thực hành nhiều, bạn càng thuần thục.

{width=800 height=419}

Những biến thể hoặc trường hợp đặc biệt liên quan đến Công Thức Tính Hình Tròn

Ngoài hình tròn đầy đủ, chúng ta còn gặp các phần của hình tròn hoặc các hình được tạo thành từ hình tròn. Việc tính toán chu vi và diện tích của chúng cũng dựa trên các công thức tính hình tròn cơ bản.

Diện Tích Hình Quạt Tròn

Hình quạt tròn là một phần của hình tròn được giới hạn bởi hai bán kính và cung tròn nối hai đầu bán kính đó. Tưởng tượng một chiếc bánh pizza tròn được cắt thành một lát, lát bánh đó chính là hình quạt.

Để tính diện tích hình quạt, chúng ta cần biết bán kính r của hình tròn và góc ở tâm (α) của hình quạt đó. Góc ở tâm có thể đo bằng độ hoặc radian.

Công thức tính diện tích hình quạt:

• Nếu góc α đo bằng độ: *S_quạt = (α / 360) πr²**
  • Đây là tỷ lệ giữa góc của hình quạt so với toàn bộ góc 360 độ của hình tròn, nhân với diện tích của cả hình tròn.
• Nếu góc α đo bằng radian: S_quạt = (1/2) r² α

Ví dụ: Tính diện tích lát bánh pizza có bán kính 20 cm và góc ở tâm 45 độ.
S_quạt = (45 / 360) 3.14 (20cm)² = (1/8) 3.14 400 cm² = 157 cm².

{width=800 height=499}

Diện Tích Hình Vành Khuyên

Hình vành khuyên là khu vực nằm giữa hai đường tròn đồng tâm (có cùng tâm nhưng khác bán kính). Tưởng tượng một chiếc đĩa CD hoặc một chiếc vòng tròn, phần vật liệu tạo nên chúng chính là hình vành khuyên.

Để tính diện tích hình vành khuyên, chúng ta cần biết bán kính của đường tròn lớn (R) và bán kính của đường tròn nhỏ (r).

Công thức tính diện tích hình vành khuyên:

S_vành khuyên = S_lớn – S_nhỏ = πR² – πr² = π(R² – r²)

Ví dụ: Một chiếc vòng trang sức có đường kính ngoài là 8 cm và đường kính trong là 6 cm. Tính diện tích bề mặt của chiếc vòng.
Bán kính ngoài R = 8cm / 2 = 4 cm.
Bán kính trong r = 6cm / 2 = 3 cm.
S_vành khuyên = 3.14 (4² – 3²) cm² = 3.14 (16 – 9) cm² = 3.14 * 7 cm² = 21.98 cm².

Độ Dài Cung Tròn

Cung tròn là một phần của đường tròn. Tương tự như hình quạt, để tính độ dài cung tròn, chúng ta cần biết bán kính r của hình tròn và góc ở tâm (α) chắn cung đó.

Công thức tính độ dài cung tròn (L):

• Nếu góc α đo bằng độ: *L = (α / 360) 2πr**
  • Đây là tỷ lệ giữa góc của cung tròn so với toàn bộ góc 360 độ, nhân với chu vi của cả hình tròn.
• Nếu góc α đo bằng radian: *L = r α**

Ví dụ: Một đường ray xe lửa được uốn cong theo hình cung tròn có bán kính 500 mét và góc chắn cung là 30 độ. Tính chiều dài của đoạn đường ray này.
L = (30 / 360) 2 3.14 500 mét = (1/12) 3140 mét = 261.67 mét (xấp xỉ).

Hiểu rõ các biến thể này giúp bạn giải quyết được nhiều bài toán phức tạp hơn trong thực tế, không chỉ dừng lại ở việc tính toán cho hình tròn đầy đủ.

Lịch sử phát triển của Công Thức Tính Hình Tròn

Hành trình khám phá ra công thức tính hình tròn là một câu chuyện dài và đầy hấp dẫn trong lịch sử toán học, kéo dài hàng nghìn năm.

Những ghi chép sớm nhất về việc tính toán liên quan đến hình tròn xuất hiện từ các nền văn minh cổ đại. Người Ai Cập cổ đại (khoảng 1650 TCN) đã có phương pháp tính diện tích hình tròn dựa trên một giá trị xấp xỉ của Pi. Trong cuộn giấy cói Rhind nổi tiếng, họ đưa ra công thức tính diện tích hình tròn bằng cách lấy đường kính trừ đi 1/9 của nó rồi bình phương kết quả. Công thức này tương đương với việc sử dụng một giá trị Pi xấp xỉ là (16/9)² ≈ 3.1605, khá gần với giá trị thực.

Người Babylon (khoảng 1900-1600 TCN) cũng sử dụng một giá trị Pi xấp xỉ 3. Họ tính chu vi bằng 3 lần đường kính và diện tích bằng (1/12) lần bình phương chu vi (tương đương với Pi = 3).

Đóng góp quan trọng nhất đến từ Hy Lạp cổ đại, đặc biệt là Archimedes xứ Syracuse (287–212 TCN). Ông không chỉ đưa ra phương pháp tính Pi bằng cách nội tiếp và ngoại tiếp các đa giác đều như đã nói ở trên, mà còn chứng minh được rằng diện tích của một hình tròn bằng diện tích của một tam giác vuông có một cạnh góc vuông bằng bán kính hình tròn và cạnh góc vuông còn lại bằng chu vi hình tròn. Từ đó, ông suy ra công thức diện tích S = (1/2) r (2πr) = πr². Phương pháp của ông là nền tảng cho việc tính toán diện tích và chu vi hình tròn một cách chính xác hơn.

Trong suốt nhiều thế kỷ sau đó, các nhà toán học ở khắp nơi trên thế giới (Ấn Độ, Trung Quốc, thế giới Hồi giáo) tiếp tục nghiên cứu và tính toán giá trị của Pi với độ chính xác ngày càng cao, từ đó củng cố thêm niềm tin vào các công thức tính hình tròn đã được tìm ra. Ký hiệu “π” cho hằng số này được nhà toán học người Wales William Jones giới thiệu vào năm 1706 và trở nên phổ biến nhờ công trình của Leonhard Euler vào thế kỷ 18.

Ngày nay, với sự phát triển của máy tính, giá trị của Pi đã được tính đến hàng nghìn tỷ chữ số sau dấu phẩy, nhưng các công thức cơ bản về chu vi và diện tích do những nhà toán học tiền bối khám phá vẫn là trụ cột cho mọi tính toán liên quan đến hình tròn. Hiểu về lịch sử này giúp chúng ta trân trọng hơn những kiến thức mà chúng ta đang sử dụng hàng ngày.

Những sai lầm thường gặp khi sử dụng Công Thức Tính Hình Tròn và cách khắc phục

Mặc dù các công thức tính hình tròn khá đơn giản, nhưng không ít người vẫn mắc phải sai lầm khi áp dụng chúng. Nhận biết và tránh những sai lầm này sẽ giúp bạn tính toán chính xác hơn.

1. Nhầm lẫn giữa Bán kính (r) và Đường kính (d)

Đây là sai lầm phổ biến nhất. Đường kính gấp đôi bán kính (d = 2r). Khi đề bài cho đường kính nhưng bạn lại dùng giá trị đó thay cho bán kính trong công thức (hoặc ngược lại), kết quả sẽ sai hoàn toàn.

• Cách khắc phục: Luôn đọc kỹ đề bài. Xác định rõ ràng con số được cho là bán kính hay đường kính. Nếu là đường kính, hãy chia đôi để có bán kính trước khi áp dụng công thức diện tích S = πr² hoặc công thức chu vi C = 2πr. Nếu là bán kính, hãy nhân đôi để có đường kính nếu cần dùng công thức C = πd.

{width=800 height=565}

2. Sử dụng sai công thức (Chu vi thay cho Diện tích hoặc ngược lại)

Công thức chu vi (C = 2πr) dùng để tính độ dài đường viền, còn công thức diện tích (S = πr²) dùng để tính bề mặt bên trong. Mỗi công thức có ứng dụng riêng.

• Cách khắc phục: Hiểu rõ ý nghĩa của từng đại lượng cần tính. Nếu đề bài hỏi về “độ dài”, “đường viền”, “quây quanh”, “dây đai”, “chu vi”… thì dùng công thức Chu vi. Nếu đề bài hỏi về “bề mặt”, “phủ kín”, “sơn”, “diện tích”, “không gian chiếm chỗ”… thì dùng công thức Diện tích. Đơn vị đo cũng là gợi ý: độ dài (cm, m) cho chu vi, diện tích (cm², m²) cho diện tích.

3. Sử dụng giá trị Pi không phù hợp hoặc làm tròn sai

Việc sử dụng Pi = 3 hoặc 3.14 thay vì giá trị chính xác hơn khi cần độ chính xác cao có thể dẫn đến sai số đáng kể. Ngược lại, đôi khi làm tròn quá sớm trong quá trình tính toán cũng gây sai lệch.

• Cách khắc phục: Kiểm tra yêu cầu về độ chính xác của bài toán. Đối với bài toán thông thường, 3.14 hoặc 22/7 là đủ. Đối với bài toán kỹ thuật, hãy sử dụng giá trị Pi từ máy tính. Chỉ làm tròn kết quả cuối cùng theo yêu cầu (ví dụ: làm tròn đến 2 chữ số thập phân).

4. Sai sót trong tính toán (nhân, chia, bình phương)

Đôi khi sai lầm chỉ đơn giản là do bấm máy tính sai hoặc tính nhẩm sai.

• Cách khắc phục: Luôn kiểm tra lại các bước tính toán, đặc biệt là phép bình phương (nhân số đó với chính nó, không phải nhân với 2). Sử dụng máy tính cẩn thận.

5. Quên kiểm tra đơn vị cuối cùng

Tính toán ra con số đúng nhưng ghi sai đơn vị (ví dụ: ghi 10 m thay vì 10 m²) là một lỗi sai thường gặp, đặc biệt trong các bài kiểm tra.

• Cách khắc phục: Luôn ghi đơn vị vào mỗi bước tính toán và đảm bảo đơn vị của kết quả cuối cùng phù hợp với đại lượng bạn đang tính (cm, m, km cho chu vi; cm², m², km² cho diện tích).

Việc chú ý đến những chi tiết nhỏ này sẽ giúp bạn tự tin hơn khi áp dụng công thức tính hình tròn vào mọi bài toán từ đơn giản đến phức tạp. Nó cũng giống như việc kiểm tra lại mã bưu chính hà nội trước khi gửi thư vậy, một chút cẩn thận có thể giúp bạn tránh được những rắc rối không đáng có.

{width=800 height=640}

Lời khuyên từ Chuyên gia về Công Thức Tính Hình Tròn

Để có thêm góc nhìn từ những người ứng dụng toán học vào thực tế, chúng ta cùng nghe chia sẻ từ Anh Nguyễn Văn An, một kỹ sư cơ khí dày dạn kinh nghiệm:

“Trong công việc của tôi, từ thiết kế các bộ phận máy cho đến tính toán vật liệu, công thức tính hình tròn xuất hiện gần như mỗi ngày. Nó là kiến thức nền tảng cực kỳ quan trọng. Điều tôi luôn nhấn mạnh với các kỹ sư trẻ là đừng bao giờ coi thường những công thức cơ bản này. Hiểu sâu sắc ý nghĩa của Pi, của bán kính, và cách chúng liên hệ với chu vi, diện tích sẽ giúp bạn giải quyết các bài toán phức tạp hơn rất nhiều sau này, ví dụ như tính thể tích hình trụ hay diện tích bề mặt hình cầu. Hơn nữa, việc rèn luyện tính cẩn thận khi áp dụng công thức, kiểm tra đơn vị, và luôn tự hỏi ‘Kết quả này có hợp lý không?’ là những thói quen tốt mà bạn sẽ dùng được trong mọi lĩnh vực, không chỉ riêng toán học hay cơ khí.”

Lời khuyên từ anh An cho thấy rằng, dù công thức có vẻ đơn giản, nhưng việc nắm vững chúng và rèn luyện kỹ năng áp dụng cẩn thận là chìa khóa thành công trong nhiều ngành nghề.

{width=800 height=419}

Mở rộng: Mối liên hệ của Công Thức Tính Hình Tròn với các lĩnh vực khác

Toán học, đặc biệt là hình học, có mối liên hệ mật thiết với rất nhiều lĩnh vực trong cuộc sống và công việc. Các công thức tính hình tròn không chỉ gói gọn trong sách vở mà còn là một phần của bức tranh lớn hơn về cách chúng ta hiểu và đo lường thế giới.

Trong lĩnh vực xuất nhập khẩu, dù có vẻ xa vời, nhưng các nguyên tắc toán học cơ bản vẫn hiện diện. Ví dụ, khi tối ưu hóa việc xếp hàng hóa có hình dạng khác nhau (bao gồm cả hình trụ, cuộn tròn…) vào container, người ta cần tính toán diện tích đáy hoặc thể tích để đảm bảo sử dụng không gian hiệu quả nhất. Việc này đòi hỏi hiểu biết về hình học, bao gồm cả công thức tính hình tròn để xử lý các vật thể có tiết diện tròn. Tối ưu hóa không gian là một phần quan trọng giúp tiết kiệm chi phí vận chuyển, một yếu tố ảnh hưởng trực tiếp đến giá thành hàng hóa và cuối cùng là cán cân xuất nhập khẩu của quốc gia.

Ngoài ra, khả năng phân tích và tính toán từ các bài tập toán học như công thức tính hình tròn rèn luyện cho chúng ta kỹ năng xử lý số liệu, điều cần thiết trong việc phân tích thị trường, tính toán chi phí, thuế, và lợi nhuận trong kinh doanh quốc tế. Việc làm quen với các công thức và quy trình tính toán từ những khái niệm cơ bản như hình tròn giúp xây dựng nền tảng cho việc hiểu và áp dụng các công thức phức tạp hơn trong kinh tế và thương mại.

Hay như việc tính toán quy mô dân số hay phân bố dân cư. Để hiểu được tỉ lệ dân thành thị hay mật độ dân số trong một khu vực, chúng ta cần tính toán diện tích của khu vực đó. Nếu khu vực đó được mô tả bởi một ranh giới hình tròn (ví dụ: vùng ảnh hưởng của một nhà máy, một công trình), công thức diện tích hình tròn sẽ được áp dụng. Thậm chí, việc lập kế hoạch logistics hay vận chuyển hàng hóa đến các địa điểm cụ thể cũng có thể liên quan đến việc tính toán khoảng cách hoặc vùng phủ sóng, đôi khi được mô hình hóa bằng các hình tròn.

Các kỹ năng cơ bản như đọc hiểu, phân tích, và áp dụng công thức không chỉ hữu ích trong toán học mà còn cần thiết trong giao tiếp chuyên nghiệp, chẳng hạn như khi bạn cần soạn thảo một email kinh doanh hiệu quả. Dù không liên quan trực tiếp đến tính toán hình tròn, nhưng sự rõ ràng, logic và chính xác trong cách viết email tiếng anh cũng phản ánh tư duy mạch lạc được rèn luyện từ việc giải quyết các bài toán có công thức.

Việc sử dụng các thông tin địa lý như mã bưu chính hà nội để xác định vị trí và lập kế hoạch vận chuyển cũng là một ví dụ về cách dữ liệu và thông tin (tương tự như bán kính hay đường kính trong công thức hình tròn) được sử dụng để giải quyết một vấn đề thực tế trong logistics.

Tóm lại, việc học và hiểu các công thức tính hình tròn không chỉ mang lại kiến thức toán học đơn thuần mà còn giúp phát triển tư duy phản biện, khả năng giải quyết vấn đề, và sự cẩn thận trong tính toán – những kỹ năng quý báu áp dụng được trong rất nhiều khía cạnh của cuộc sống và công việc, bao gồm cả những lĩnh vực tưởng chừng không liên quan như xuất nhập khẩu hay logistics.

{width=800 height=420}

Kết bài

Như vậy, chúng ta đã cùng nhau khám phá hành trình thú vị của công thức tính hình tròn, từ định nghĩa cơ bản, nguồn gốc lịch sử, cách áp dụng chi tiết cho cả chu vi và diện tích, các trường hợp đặc biệt, đến những sai lầm cần tránh và mối liên hệ bất ngờ với các lĩnh vực khác trong cuộc sống và công việc.

Chúng ta đã nhắc lại rằng, chu vi hình tròn được tính bằng C = 2πr hoặc C = πd, còn diện tích hình tròn được tính bằng S = πr². Những công thức này, tưởng chừng đơn giản, lại là chìa khóa để giải quyết vô số bài toán thực tế và là nền tảng cho nhiều ngành khoa học, kỹ thuật.

Việc nắm vững công thức tính hình tròn không chỉ giúp bạn vượt qua các bài kiểm tra toán mà quan trọng hơn, nó trang bị cho bạn khả năng quan sát, phân tích và định lượng thế giới xung quanh. Từ việc ước lượng lượng sơn cần dùng cho chiếc thùng phi hình tròn đến tính toán diện tích cần lát gạch cho đài phun nước, kiến thức này luôn hiện hữu và hữu ích.

Đừng ngần ngại thực hành tính toán với các vật thể hình tròn quanh bạn. Hãy thử đo đường kính của chiếc đĩa, chiếc cốc, hoặc chiếc bánh xe và tự mình tính toán chu vi và diện tích của chúng. Càng thực hành, bạn càng ghi nhớ công thức và áp dụng chúng một cách tự tin, chính xác hơn.

Hy vọng bài viết này đã mang đến cho bạn những thông tin hữu ích và truyền cảm hứng để nhìn nhận những kiến thức toán học cơ bản như công thức tính hình tròn một cách mới mẻ và ứng dụng hơn trong cuộc sống hàng ngày. Cảm ơn bạn đã đồng hành cùng Tài Liệu XNK khám phá chủ đề này!